Fatia de pizza – Você pega uma fatia de pizza e está prestes a dar uma mordida, mas ela cai e balança nos dedos. A crosta não é rígida o suficiente para suportar o peso da fatia.
Mas não há necessidade de se desesperar, pois anos de experiência em comer uma fatia de pizza lhe ensinaram como lidar com essa situação. Basta dobrar a fatia de pizza em forma de U (também conhecida como dobra ). Isso evita que a fatia caia e você pode desfrutar da sua refeição. (Se você não tem uma fatia de pizza à mão, pode experimentar com uma folha de papel.)
Porque dobrar uma fatia de pizza ajuda você a comer? Aprofunde-se nessa matemática da fatia de pizza.
Pendure uma folha de papel e ela cai, mas dê uma dobra e ela fica rígida. Por quê?
Por trás desse truque da fatia de pizza está um poderoso resultado matemático sobre superfícies curvas, tão surpreendente que seu descobridor, o gênio matemático Carl Friedrich Gauss , nomeou-o Theorema Egregium , em latim, para teorema excelente ou notável.
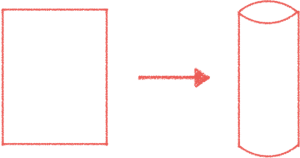
Pegue uma folha de papel e enrole-a em um cilindro. Pode parecer óbvio que o papel é plano, enquanto o cilindro é curvado. Mas Gauss pensou sobre isso de forma diferente. Ele queria definir a curvatura de uma superfície de uma maneira que não muda quando você dobra a superfície.
Se você aproximar uma formiga que mora no cilindro, há muitos caminhos possíveis que a formiga pode seguir. Podia decidir percorrer o caminho curvo, traçar um círculo ou percorrer o caminho plano, traçando uma linha reta. Ou pode fazer algo no meio, traçando uma hélice.
Cadastre seu e-mail para receber todas as nossas novidades
O insight brilhante de Gauss era definir a curvatura de uma superfície de uma maneira que levasse todas essas escolhas em consideração. Veja como isso funciona. A partir de qualquer ponto, encontre os dois caminhos mais extremos que uma formiga pode escolher (ou seja, o caminho mais côncavo e o caminho mais convexo). Em seguida, multiplique a curvatura desses caminhos juntos (a curvatura é positiva para caminhos côncavos, zero para caminhos planos e negativa para caminhos convexos). E, voila, o número que você recebe é a definição de Gauss da curvatura naquele ponto.
Vamos tentar alguns exemplos. Para a formiga no cilindro, os dois caminhos extremos disponíveis para ela são o caminho curvo, em forma de círculo, e o caminho plano e reto. Mas como o caminho plano tem curvatura zero, quando você multiplica as duas curvaturas juntas, obtém zero. Como os matemáticos diriam, um cilindro é plano – tem curvatura zero de Gauss . O que reflete o fato de que você pode rolar um de uma folha de papel.
Se, em vez disso, a formiga vivesse em uma bola, não haveria caminhos planos disponíveis para ela. Agora, cada caminho se curva na mesma quantidade e, portanto, a curvatura de Gauss é um número positivo. Então as esferas são curvas enquanto os cilindros são planos. Você pode dobrar uma folha de papel em um tubo, mas nunca pode dobrá-lo em uma bola.
O notável teorema de Gauss, o que eu gosto de imaginar o fez rir de alegria, é que uma formiga vivendo em uma superfície pode trabalhar sua curvatura sem nunca ter que sair da superfície, apenas medindo distâncias e fazendo alguma matemática.
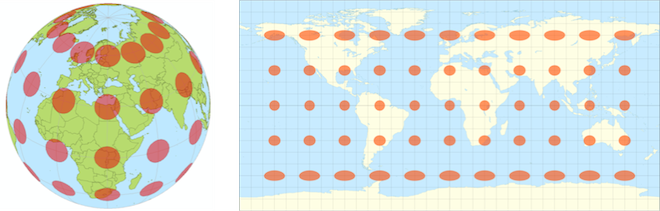
Outra consequência do teorema de Gauss é que é impossível retratar com precisão um mapa no papel. O mapa do mundo que você está acostumado a ver descreve os ângulos corretamente, mas distorce grosseiramente as áreas. O Museu da Matemática ressalta que os designers de roupas têm um desafio semelhante – eles projetam padrões em uma superfície plana que deve caber em nossos corpos curvos.
Círculos de tamanhos iguais desenhados em um globo tornam-se distorcidos em um atlas.
O que isso tem a ver com pizza? Bem, a fatia de pizza era plana antes de você pegá-lo (em matemática, tem zero curvatura de Gauss). O notável teorema de Gauss nos assegura que uma direção da fatia deve permanecer sempre plana – não importa como você a dobra, a fatia de pizza deve manter um traço de sua planicidade original.
Quando a fatia cai, a direção plana (mostrada em vermelho abaixo) é apontada para o lado, o que não é útil para comê-la. Mas, dobrando a fatia de pizza para o lado, você está forçando-a a ficar plana na outra direção – a que aponta para a sua boca. Theorema egregium, na verdade.
Quem sabia que a geometria poderia ser tão deliciosa?

Encurvando uma folha em uma direção, você a força a ficar dura na outra direção. Depois de reconhecer essa ideia, você começa a vê-la em todos os lugares.
Engenheiros freqüentemente usam curvatura para adicionar força às estruturas. No autódromo de Zarzuela, em Madri, o engenheiro estrutural espanhol Eduardo Torroja projetou um inovador teto de concreto que se estende do estádio, cobrindo uma grande área, com apenas alguns centímetros de espessura. É o truque da pizza disfarçado.
Depois de reconhecer o truque da pizza, você começa a vê-lo em todos os lugares.
Talvez o exemplo mais mundano de força através da curvatura sejam os materiais de construção corrugados onipresentes (o corrugado vem do ruga, o latim para o enrugamento). Você dificilmente poderia ficar mais sem graça do que uma caixa de papelão ondulada . Destrua uma dessas caixas e você encontrará uma onda familiar e ondulada de papelão dentro das paredes. As rugas não estão lá por quaisquer razões estéticas. Eles são uma maneira engenhosa de manter um material fino e leve, mas rígido o suficiente para resistir à flexão sob cargas consideráveis.
Uma folha de papel colocada em dois livros não suporta nem o peso de um lápis. Mas se você corrugar a folha dobrando-a algumas vezes, ela suportará uma lata de feijão!
Eles simplesmente não escrevem revistas de arquitetura como costumavam fazer.
Faça um teste vá até a geladeira e pegue um ovo. Coloque-o na palma da sua mão, envolva seus dedos ao redor do ovo e aperte. (Certifique-se de que você não está usando um anel se você tentar isso.) Você ficará surpreso com a sua força. Não consegui esmagar o ovo e dei tudo o que tinha. (Sério, você precisa tentar isso para acreditar.)
Tente fazer isso em casa. (Talvez em cima de uma pia só para ficar seguro.)
O que faz os ovos tão fortes? Bem, latas de refrigerante e chapas de metal corrugado são curvas em uma direção, mas planas na outra. Essa curvatura lhes confere alguma rigidez, mas eles ainda podem ser achatados nas folhas planas de onde vieram.
Em contraste, as cascas de ovos são curvas em ambas as direções. Esta é a chave para a força de um ovo. Expressas em termos matemáticos, estas superfícies duplamente curvas possuem curvatura Gaussiana não nula.
Para quebrar um ovo aberto, você primeiro precisa amassar. Quando o ovo perde sua curvatura, perde sua força.
A forma icônica de uma torre de resfriamento de uma usina nuclear também incorpora curvatura em ambas as direções. Essa forma, chamada hiperbolóide , minimiza a quantidade de material necessária para construí-la. As chaminés regulares são muito parecidas com latas de refrigerante gigantes – elas são fortes, mas também podem se dobrar facilmente. Uma chaminé em forma de hiperboloide resolve este problema curvando-se em ambas as direções. Esta curvatura dupla fixa a forma no lugar, dando-lhe rigidez extra que falta uma chaminé regular.
Força através da curvatura é uma ideia que molda o nosso mundo e tem suas raízes na geometria. Então, da próxima vez que você pegar uma fatia, reserve um momento para olhar em volta e apreciar o vasto legado por trás desse simples truque de pizza.
Referências
Reid, Esmond. Compreensão de edifícios: uma abordagem multidisciplinar . MIT Press, 1984.
[1] Mornement, Adam e Simon Holloway. Ferro ondulado: construindo na fronteira . WW Norton & Company, 2007.
Garlock, Maria E. Moreyra, David P. Billington e Noah Burger. Félix Candela: engenheiro, construtor, artista estrutural. Museu de Arte da Universidade de Princeton, 2008.
* De acordo com uma decisão da FDA, os Pringles não são legalmente batatas fritas porque são feitos de flocos de batata secos.
Nos siga nas redes sociais!